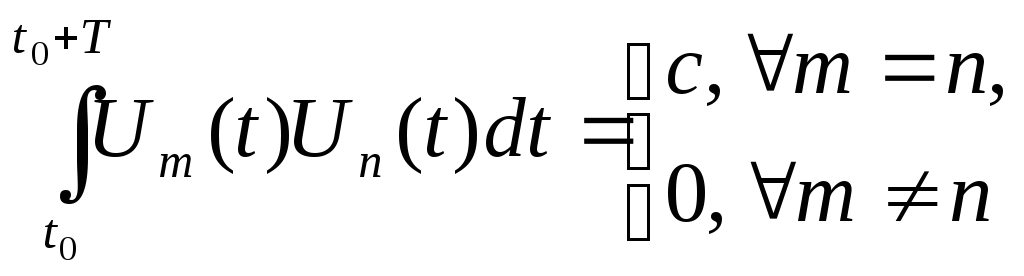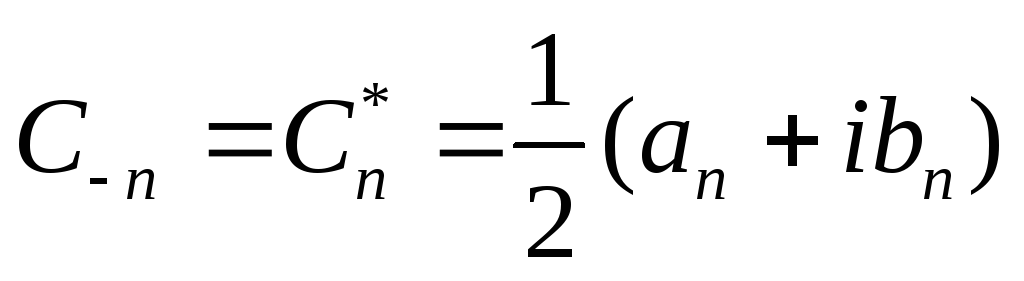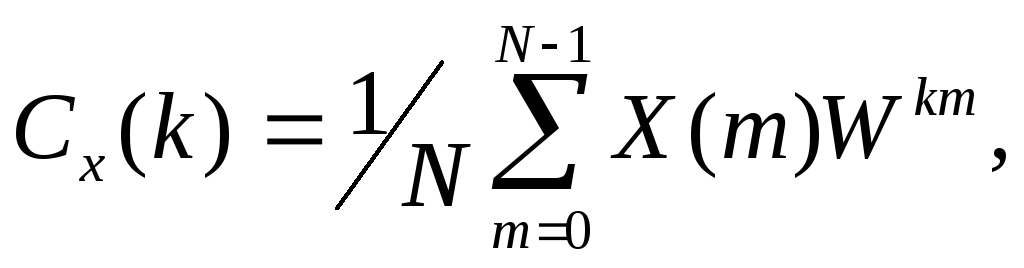Содержание

Как Сделать Преобразование Фурье в Excel

прямое или обратное Быстрое Преобразование Фурье вектора, матрицы или гиперматрицы

Синтаксис

Аргументы

A, X векторы, матрицы или многомерные массивы вещественных или комплексных чисел одинаковых размеров.

sign -1 или 1 : знак множителя ±2iπ в экспоненциальном члене формулы преобразования, устанавливающий прямое или обратное преобразование. По умолчанию значение равно -1 , соответствующее прямому преобразованию.

directions вектор, содержащий индексы размерности A (в [1, ndims(A)] ) вдоль которой необходимо вычислить БПФ (многомерный). По умолчанию направления directions соответствуют 1:ndims(A) : «кумулятивный» БПФ вычисляется для всех направлений. См. раздел «Описание».

«symmetric»

Многомерный массив B размерами [s1,s2. sN] сопряжённо симметричный для БПФ, если и только если B==conj(B([1 s1:-1:2],[1 s2:-1:2]. [1 sN:-1:2])) . В этом случае результат X является вещественным и может использоваться эффективный специфический алгоритм для его вычисления.

dims вектор положительных целых чисел. Старый синтаксис. Каждый элемент должен быть делителем length(A) . Произведение элементов должно быть строго меньше length(A) . См. подробности в разделе «Описание».

incr вектор положительных строго возрастающих целых чисел, такой же длины, что и dims . Старый синтаксис. Каждый элемент должен быть делителем length(A) . См. подробности в разделе «Описание».

Описание

Эта функция вычисляет прямое или обратное одно-, дву- или многомерное дискретное преобразование Фурье массива или многомерного массива чисел вдоль одного или нескольких направлений внутри этого массива.

Краткий синтаксис

X = fft(A [,symmetry]) или X = fft(A, -1 [,symmetry]) выполняет прямое преобразование. одномерное a=A является вектором: вычисляется одномерное прямое БПФ, так что:

многомерное A является матрицей или многомерным массивом: выполняется многомерное прямое БПФ.

X = fft(A,+1) или X = ifft(A) выполняет обратное нормированное преобразование, такое, что A==ifft(fft(A)) . одномерное a=A является вектором: X = fft(a, +1) или X = ifft(a) выполняют одномерное обратное БПФ, вычисляемое как:

многомерное A является матрицей или многомерным массивом: выполняется многомерное обратное БПФ.

Длинный синтаксис: многомерное прямое БПФ

Например, если A является трёхмерным массивом, то X = fft(A,-1,2) эквивалентно:

Например, если A является массивом с n1*n2*n3 элементов, X = fft(A,-1, n1, 1) эквивалентно X = fft(matrix(A,[n1,n2,n3]), -1, 1) ; а X = fft(A,-1, [n1 n3], [1 n1*n2]) эквивалентно X = fft(matrix(A,[n1,n2,n3]), -1, [1,3]) .

Оптимизация fft

Примечание: Функция fft() автоматически сохраняет свои последние внутренние параметры в памяти для повторного их использования во второй раз. Это значительно улучшает время вычисления, когда выполняются последовательные вызовы (с одинаковыми параметрами).

Можно пойти дальше в оптимизации fft() , используя функции get_fftw_wisdom и set_fftw_wisdom.

[expert_bq id=»1570″]входной поток поступает на небольшое FIFO на частоте обработки и преобразуется в поток на частоте контроллера памяти например, 333 МГц. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq] Чем выше порядок оконной функции — тем ниже уровень боковых лепестков спектра. На практике мне приходилось использовать окна до 5 порядка. Останавливаться на этом не будем, более подробно об оконной фильтрации на ПЛИС я уже рассказывал в своей предыдущей статье.

Как Сделать Преобразование Фурье в Excel • Оконная функция

Быстрое преобразование Фурье

б) теорема комплексной сопряженности: если X(m)>=X(0), X(1),… ,X(N-1)> – такая последовательность действительных чисел, что N/2 – целое число и X(m)C_x(k), то

Лабораторная работа №1 Преобразование Фурье

Изучение преобразования Фурье и его основных свойств, а также методики получения быстрого преобразования Фурье (БПФ).

Теоретические сведения

Для лучшего понимания вопроса о рядах Фурье дадим определение ортогональным функциям. Множество непрерывных функций действительного переменного называется ортогональным на интервале , если

(1.1)

При множество U_n(t)> называется ортонормированным.

Для теории формирования и обработки сигнала особое значение имеет возможность разложения заданного в виде функции сигнала по различным ортогональным системам функций.

Впервые в 1807 году французский математик и физик Жан Батист Жозеф Фурье показал, что любую произвольную функцию можно представить в виде бесконечной суммы синусных и косинусных членов:

, (1.2)

Коэффициенты a₀, a_n, b_n> из формулы (1.2) можно вычислить с учетом ортогональности множества функций cos n₀t, sin n₀t> на периоде T:

(1.3)

(1.4)

(1.5)

(1.6)

(1.7)

. (1.8)

Раздел математики, устанавливающий соотношение между функцией и коэффициентами и , называется гармоническим анализом, а представление (1.2) – рядом Фурье.

Компоненты ряда Фурье называются гармониками. Любая четная функция может быть разложена в ряд Фурье, состоящий из косинусов, а любая нечетная функция раскладывается в ряд из синусов. Для некоторых функций ряд Фурье может состоять лишь из нечетных гармоник.

В целом, любая полная система ортогональных функций может быть применена для разложения в ряды, которые соответствуют рядам Фурье. Например, часто используется разложение в ряды по функциям Уолша, Хаара, Лагерра, Бесселя и т.д.

Семейство преобразований Фурье (преобразование Фурье, ряды Фурье, дискретные ряды Фурье и дискретное преобразование Фурье) представлено на рис. 1.1 – 1.4.

Рис. 1.1. Преобразование Фурье: сигнал непрерывный и апериодический

Рис. 1.2. Ряды Фурье: сигнал непрерывный и периодический

Рис. 1.3. Дискретные ряды Фурье: сигнал дискретный и апериодический

(дискретные ряды Фурье) сигнал дискретный и периодический

Основная идея ДПФ ни чем не отличается от ПФ (см. рис. 1.5).

Для получения представления x(t) (1.2) рядом Фурье в комплексной форме необходимо использовать соотношения в виде формулы Эйлера:

; . (1.9)

(1.10)

или ;

. (1.11)

. (1.12)

Таким образом, если означает последовательность X(m) конечных действительных или комплексных чисел, где , то дискретное преобразование Фурье этой последовательности определяется как

, где , , , (1.13)

. (1.14)

Выражения (1.13), (1.14) составляют пару преобразований Фурье.

Функции W km являются N-периодическими, т.е. W km =W ( k + N ) m =W k ( m + N ) .

Следовательно, последовательности C_x(k)>, также являются N-периодическими, т.е.

Рассмотрим основные свойства дискретного преобразования Фурье:

а) теорема линейности: дискретное преобразование Фурье является линейным, т.е. если , и , то ;

б) теорема комплексной сопряженности: если X(m)>=X(0), X(1),… ,X(N-1)> – такая последовательность действительных чисел, что N/2 – целое число и X(m)C_x(k), то

. (1.15)

Из (1.13) следует, что где W=e — i 2  / N .

Тогда, подставляя вместо k – (N/2+l), будем иметь

т.к. W Nm =-1.

в) теорема сдвига: если Z(m)C_z(k) и Z(m)=X(m+h), , то

C_z(k)=W — kh C_x(k). (1.16)

Z(m)C_z(k), т.е. , .

С учетом подстановки Z(m)=X(m+h), будем иметь .

Осуществляя замену переменных m+h=r, указанное соотношение будет иметь вид .

, когда p и q удовлетворяют условию

|p—q|=N-1, то C_z(k)=W — kh C_x(k).

Аналогично при Z(m)=X(m-h) , C_z(k)=W kh C_x(k).
[expert_bq id=»1570″]В целом, любая полная система ортогональных функций может быть применена для разложения в ряды, которые соответствуют рядам Фурье. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq] б) теорема комплексной сопряженности: если X(m)>=X(0), X(1),… ,X(N-1)> – такая последовательность действительных чисел, что N/2 – целое число и X(m)C_x(k), то
Дискретное преобразование Фурье

Пусть исходный дискретный сигнал ограничен во времени и содержит ненулевых отсчетов, взятых с интервалом дискретизации с. Данное предположение на практике всегда выполняется, потому что мы не можем получить бесконечное число отсчетов сигнала. Тогда длительность дискретного сигнала равна cекунд, и можно записать как:

Дополнительные данные → Похожие темы → Все про Exel → Как вставить значения → Как объединить ячейки → Как вставить форматы → Дополнительные данные → Вставить формулы→ Аргументы функции